Understanding K-means Clustering in Machine Learning Free Download
Before diving straightaway into studying the algorithmic program let us have just about background about the algorithm. K-means clustering is a Automobile Learning Algorithm. Precisely, machine learning algorithms are broadly categorized equally supervised and unsupervised. Unattended learning is further classified as a transformation of the information set and cluster. Clustering farther is of various types and K-agency lie in to hierarchical clustering.
Let us have an overview of these concepts ahead starting time to study the algorithm in detail.
What is Unsupervised Learning?
The auto is pot-trained connected unlabelled data without any guidance it should discover hidden patterns in the data. Unsupervised learning algorithms perform complex tasks but can cost more doubtful as compared with the natural learning method. Unsupervised methods allow finding features that are useful for categorization purposes. Also, all unknown patterns can be found using unsupervised encyclopaedism. The problems of unsupervised scholarship are categorized as cluster and association problems.
To know more all but unattended encyclopedism in detail confabulate Here and chequer here the difference betwixt unsupervised learning and supervised learning.
Rent out us immediately ensure what is bunch:
What is Clustering?
Let's consider a dataset of points:
![]()
We assume that it's contingent to observe a criterion (not unique) so that each sample can be associated with a specific group:
![]()
Conventionally, each aggroup is called a constellate and the cognitive process of finding the function G is called clustering. Clustering is reasoned American Samoa an important concept to deal with the finding of a structure or a pattern in a bunch of unknown data. Clustering algorithms process the data and discover natural clusters (groups) if they are present in the information. It is capable to the drug user to adjust the number of clusters an algorithm should discern as the algorithmic rule gives the world power to qualify the granularity of the group.
There are single types of clump you pot use:
- Partitioning: The data is organised such that a single data john be a part of one flock only.
- Agglomerative: Every information is a bundle in this technique.
- Overlapping: In this proficiency, fuzzy sets are used to cluster data in this technique.
- Probabilistic: Chance distribution is used in that technique to make the clump.
- Hierarchical: This algorithm makes a power structure of clusters. It begins with all the information allotted to the cluster of their own. So deuce clusters are exit to follow in the same cluster the algorithmic rule comes to goal when just a single cluster is left.
- K-mean Clustering: K refers to the dull clustering algorithm that helps to find the highest value for every job. In that method acting of clustering, the required number of clusters is elite, the data points are clustered into k-groups. A bigger k-means smaller groups with much granularity whereas a smaller k means bigger groups with a reduced amount of granularity.
Net ball us now study the k-means clustering algorithmic rule in detail:
K- Means Bunch Algorithm
The k-means algorithm is based on the first condition to decide the number of clusters through the appointment of k initial centroids or means:
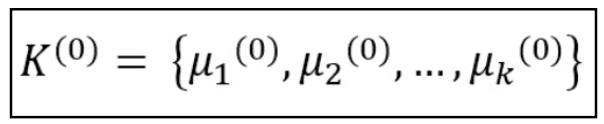
Then the distance 'tween each sample distribution and each centroid is computed and the sample is appointed to the cluster where the distance is minimum. This approach is often called minimizing the inactiveness of the clusters, which is defined as follows:
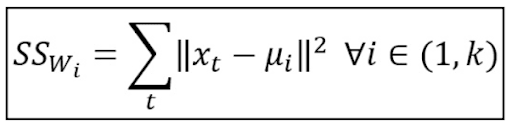
The process is iterative, erst all the samples have been processed, a new set of centroids K is computed and all the distances are recomputed. The algorithm stops when the desired tolerance is reached, or in other dustup, when the centroids become stable and, therefore, the inertia is minimized.
Recursive Steps
Let X = { x 1 , x 2 , x 3 , ……, x n } be the rig of data points an
μ = {μ 1 , μ 2 , μ 3 ,........,μ n } be the centres.
- Select "C" constellate centres randomly.
- Cypher the distance between each information point and cluster centres.
- The information point with stripped outdistance from the cluster centre is assigned to the cluster centre.
- Rectangle the new cluster centre with the formula:
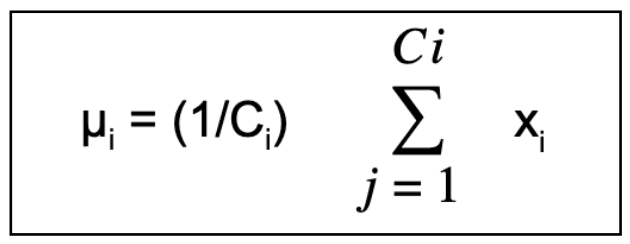
where ci represents the turn of data points in the ith cluster
- Recalculate the distance b/w new obtained cluster centres and data points.
- Terminate if no data point was reassigned, else repeat from step 3.
Sample Data Set Explaining K-means Clustering
Consider a simple example with a dummy dataset:
from sklearn.datasets import make_blobs
nb_samples = 1000
X, _ = make_blobs(n_samples=nb_samples, n_features=2, centers=3, cluster_std=1.5
In our example, we have terzetto clusters with bidimensional features and a fond convergence receivable to the standard deviation of each blob. We harbour't use the variable here as we want to bring fort a set of locally coherent points to try our algorithms:
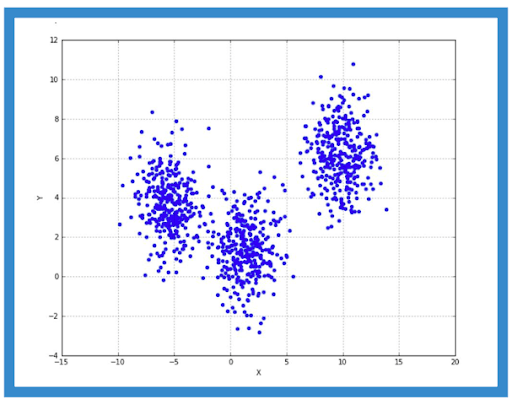
In this subject, we expect k-means to separate the three groups with minimum error in the X-area bounded betwixt [-5, 0]. Hence, keeping the nonpayment values we sustain:
from sklearn.flock import KMeans
>>> km = KMeans(n_clusters=3)
>>> km.fit(X)KMeans(algorithm='auto', copy_x=True, init='k-means++', max_iter=300,
n_clusters=3, n_init=10, n_jobs=1, precompute_distances='auto', random_state=None, tol=0.0001, verbose=0)>>> photographic print(km.cluster_centers_)
[[ 1.39014517, 1.38533993]
[ 9.78473454, 6.1946332 ]
[-5.47807472, 3.73913652]]
Reploting the data with three assorted markers, we verify how k-means successfully separated the information.
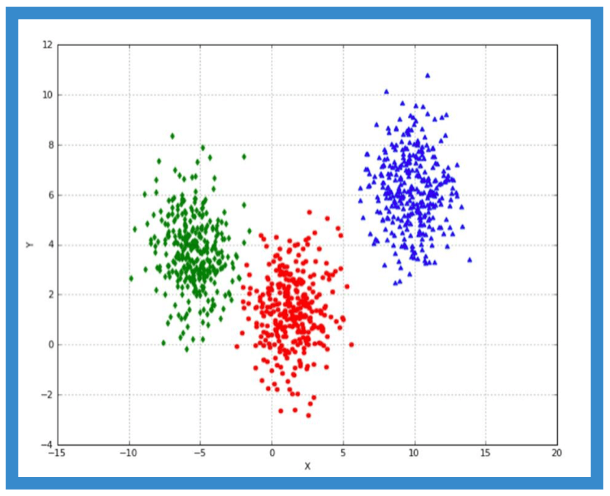
In this case, the separation is easy because k-means is based on geometer distance, which is radial and so clusters are expected to be nipple-shaped. The job can non be solved using this algorithm if all of this doesn't happen. Mostly, k-agency throne produce good results even if the convexity is non fully guaranteed, but there are individual situations when the expected clustering is impossible and rental k-substance finding tabu the centroid can lead to wrong solutions.
Let us besides consider the case of concentric circles, scikit-learn provides a inherent function to father such datasets:
from sklearn.datasets importee make_circles
>>> nb_samples = 1000
>>> X, Y = make_circles(n_samples=nb_samples, noise=0.05)
The plot for concentric circles is shown:
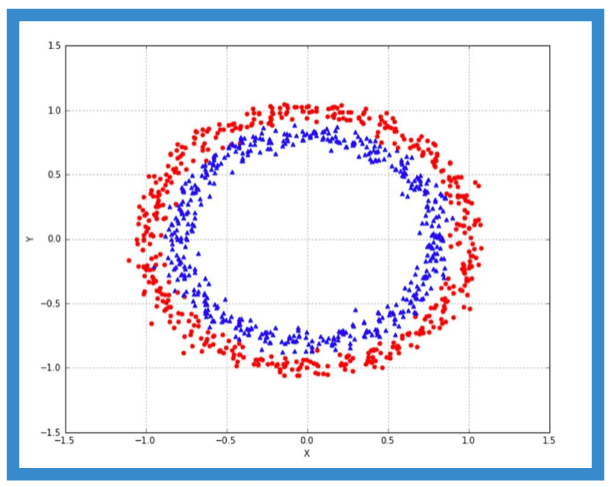
Here we have an internal clustering (blue triangle markers) and an outer peerless (red acid markers). Much sets are non lentiform, then it's unbearable for k-agency to asunder them correctly.
Suppose, we implement the algorithmic rule to two clusters:
>>> km = KMeans(n_clusters=2)
>>> km.fit(X)KMeans(algorithmic rule='auto', copy_x=True, init='k-way++', max_iter=300,
n_clusters=2, n_init=10, n_jobs=1, precompute_distances='auto', random_state=No, tol=0.0001, verbose=0)
We get the separation as shown:
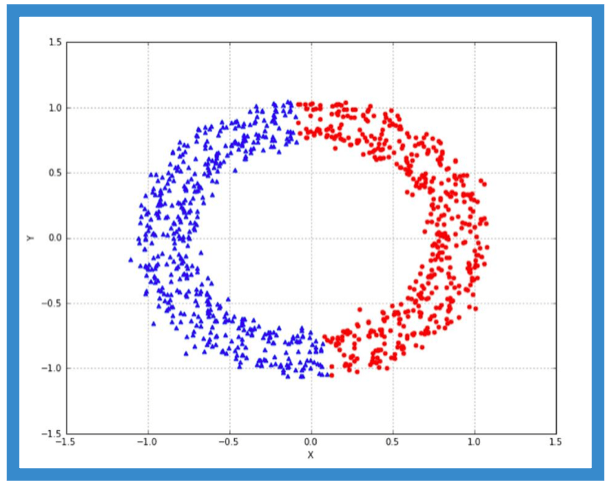
A expected, k-means converges on the two centroids in the midst of the cardinal half-circles, and the subsequent clustering is quite different.
K-means Bunch Algorithmic rule Inscribe in Python
df = pd.DataFrame({
'x': [12, 20, 28, 18, 29, 33, 24, 45, 45, 52, 51, 52, 55, 53, 55, 61, 64, 69, 72],
'y': [39, 36, 30, 52, 54, 46, 55, 59, 63, 70, 66, 63, 58, 23, 14, 8, 19, 7, 24]
})
from sklearn.cluster import KMeans
kmeans = KMeans(n_clusters=3)
kmeans.fit(df)
------------------------------------------------------------------------------labels = kmeans.predict(df)
centroids = kmeans.cluster_centers_
fig = plt.see(figsize=(5, 5))colors = map(lambda x: colmap[x+1], labels)
plt.scatter(df['x'], df['y'], colour in=colors, of import=0.5, edgecolor='k')
for idx, centroid in enumerate(centroids):
plt.scatter(*centroid, color=colmap[idx+1])
plt.xlim(0, 80)
plt.ylim(0, 80)
plt.show()
------------------------------------------------------------------------------
K-means Clustering Algorithm Code in R
# K-Means Algorithm
#k=3 # the numerate of K
max=5000 # the supreme count for generating random points
n=100 # the number of points
maxIter = 10 # maximum number of iterations
doorstep = 0.1 #difference of yellowed means and inexperienced means
# Randomly generate points in the form of (x,y)
x <- sample(1:goop, n)
y <- sample(1:grievous bodily harm, n)
# put direct into a matrix
z <- c(x,y)
m = intercellular substance(z, ncol=2)
ks <- c(1,2,4,8,10,15,20) # different Sunflower State
for(k in ks)
myKmeans(m, k, max)
myKmeans <- function(m, k, max)
{
#initialization for k means: the k-first points in the list
x <- m[, 1]
y <- m[, 2]
d=intercellular substance(data=NA, ncol=0, nrow=0)
for(i in 1:k)
d <- c(d, c(x[i], y[i]))
init <- matrix(d, ncol=2, byrow=TRUE)
dev.new()
plotTitle <- spread("K-Means Clustering K = ", k)
plot(m, xlim=c(1,max), ylim=c(1,max), xlab="X", ylab="Y", pch=20,
primary=plotTitle)
par(new=T)
patch(init, pch=2, xlim=c(1,max), ylim=c(1,max), xlab="X", ylab="Y")
equality(new=T)
oldMeans <- init
oldMeans
one hundred fifty <- Clustering(m, oldMeans)
Cl
means <- UpdateMeans(m, cl, k)
thr <- delta(oldMeans, means)
itr <- 1
while(thr > threshold)
{
cl <- Clustering(m, substance)
oldMeans <- means
substance <- UpdateMeans(m, cl, k)
thr <- delta(oldMeans, agency)
itr <- itr+1
}
cl
thr
means
itr
for(kilometer in 1:k)
{
group <- which(cl == kilometer)
plot(m[grouping,],axes=F, gap=km, xlim=c(1,liquid ecstasy), ylim=c(1,max), pch=20, xlab="X", ylab="Y")
par(new=T)
}
plot(means, axes=F, pch=8, col=15, xlim=c(1,goop), ylim=c(1,grievous bodily harm), xlab="X", ylab="Y")
par(new=T)
dev.off()
} # end function myKmeans
#function distance
dist <- function(x,y)
{
d<-sqrt( sum((x - y) **2 ))
}
createMeanMatrix <- function(d)
{
matrix(d, ncol=2, byrow=Confessedly)
}
# compute euclidean space
Euclid <- function(a,b){
d<-sqrt(a**2 + b**2)
}
euclid2 <- function(a){
d<-sqrt(sum(a**2))
}
#compute deviation between new way and old means
delta <- function(oldMeans, newMeans)
{
a <- newMeans - oldMeans
max(Euclid(a[, 1], a[, 2]))
}
Clump <- purpose(m, means)
{
clusters = c()
n <- nrow(m)
for(i in 1:n)
{
distances = c()
k <- nrow(means)
for(j in 1:k)
{
di <- m[i,] - means[j,]
darmstadtium<-euclid2(di)
distances <- c(distances, ds)
}
minDist <- Taiwanese(distances)
cl <- match(minDist, distances)
clusters <- c(clusters, centilitre)
}
return (clusters)
}
UpdateMeans <- function(m, cl, k)
{
substance <- c()
for(c in 1:k)
{
# go the pointedness of bunch c
aggroup <- which(cl == c)
# compute the mean breaker point of all points in bundle c
mt1 <- mean(m[group,1])
mt2 <- mean(m[mathematical group,2])
vMean <- c(mt1, mt2)
means <- c(means, vMean)
}
means <- createMeanMatrix(means)
reelect(means)
}
Challenges of the K-means Clustering Algorithmic rule
1. Different Cluster Size
The common take exception that the algorithmic rule faces is different cluster sizes.
Let us understand this with an example:
Consider an groundbreaking set of points as shown below:
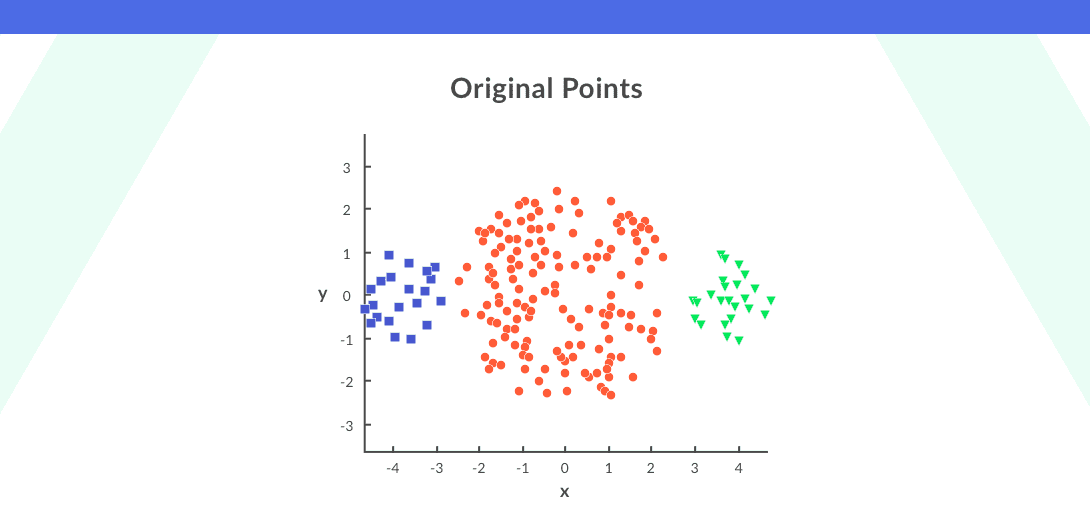
In the daring plot, the right and leftmost clusters are of smaller sizing A compared to the central cluster on applying k-means clustering on this algorithm, the result would glucinium as shown:
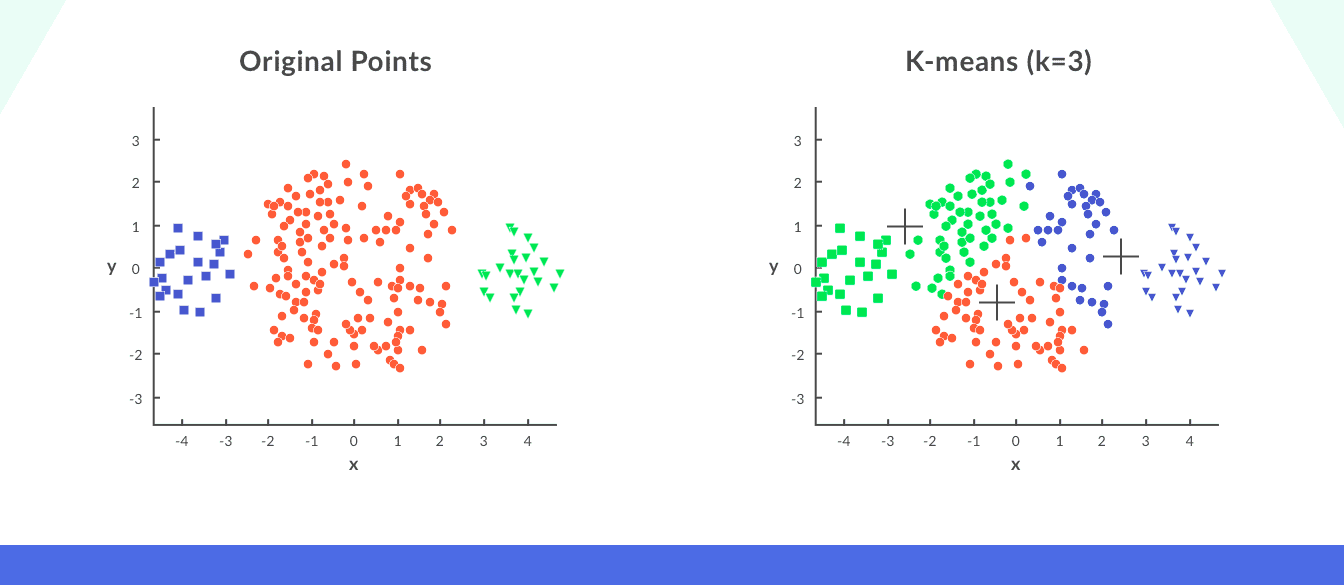
2. Different Density of Information Points
Other challenges of the algorithm arise when the densities of the primary points are different.
Consider again, a set of original points as shown:
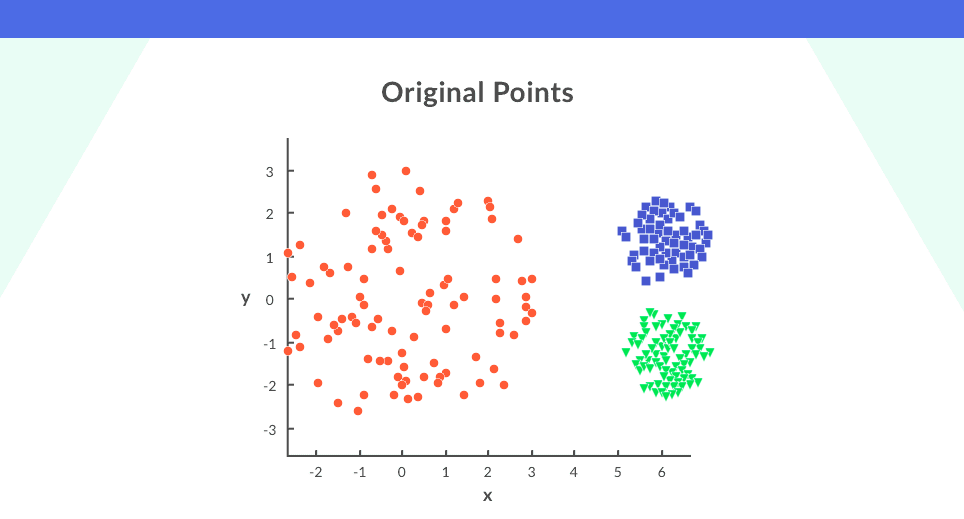
In the plot above, the points in the blue and given clusters are close packed whereas the points in the scarlet cluster are spread out on applying k-means clustering happening these points. We testament get the cluster every bit shown.
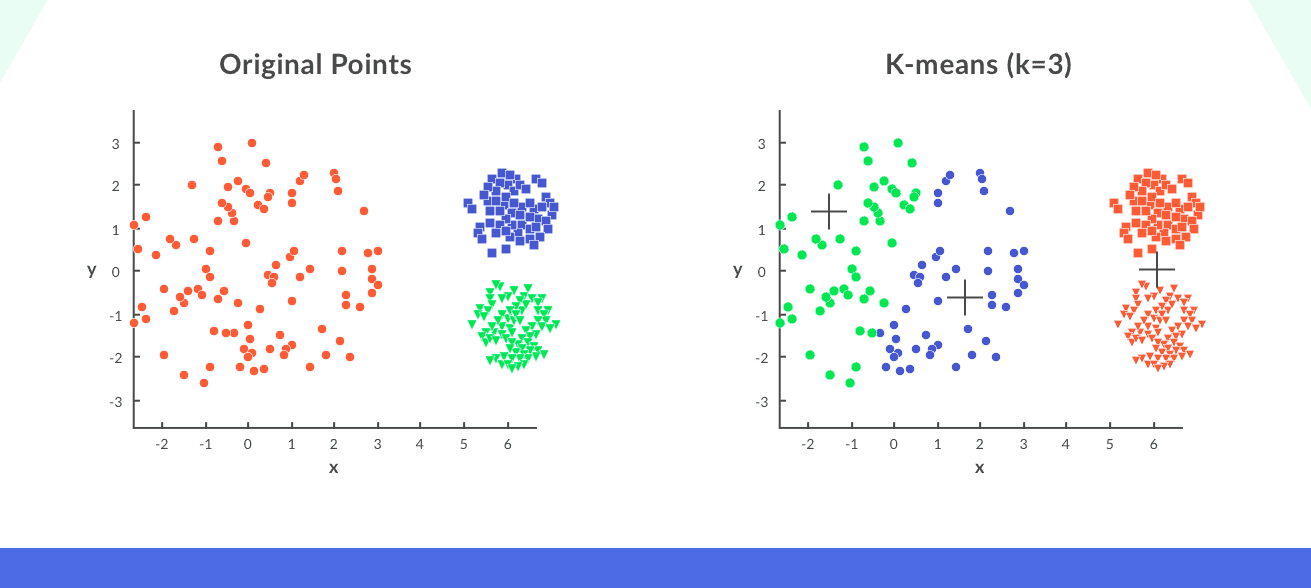
We see that the compact points have been appointed to a bingle cluster, whereas the points that were propagate out before and were in the same bundle are assigned to different clusters.
The result could exist victimisation a high number of clusters, so alternatively of three clusters (k=10) thus leading to the formation of meaningful clusters.
Applications of K-means Clustering Algorithmic rule
1. Document Classification
This is a very standard classification problem and this algorithm is considered appropriate to solve information technology. Documents are clustered in sextuple categories supported along tags, content, topics of the papers.
2. Customer Segmentation
Bunch Technique segment customers based on buy history, interests surgery activity monitoring thus helping markets to improve their customer base, work on target areas. The assortment would help the company target taxonomic group clusters of customers.
3. Insurance Fraud Sensing
It is conceivable to isolate recently claims by utilizing onetime historical information on fraudulent claims. Based on historical data clusters keister be formed indicating fraudulent.
4. Margin call Record Information Analysis
CDR is the information captured away telecom companies and is used to understand the segment of customers with respect to their usage of hours.
The information collected via calls, SMS, and the cyberspace provides greater insights about customers needs when used with the demographics of the customer.
5. Cyber Profiling Criminals
The mind of cyber profiling is derivative from criminal profiles and in the process of information accumulation from individuals and groups to identify epochal co-relations
Cyber profiling provides data on the investigation division to classify the types of criminals at the crime scene.
Advantages of K-means Clustering Algorithm
- Easy to encompass.
- Robust and fixed algorithm.
- Efficient algorithm with the complexity O(tknd) where:
- t: number of iterations.
- k: number of centroids (clusters).
- n: number of objects.
- d: property of each object.
- Normally, IT is k, t, d << n.
- IT gives the best result when the data sets are decided and well separated from apiece another.
Disadvantages of K-means Clustering Algorithm
- The algorithm requires the Apriori specification of the telephone number of cluster centres.
- The k-means cannot declaration that there are ii clusters if there are two highly overlapping data.
- The algorithm is not unvarying to not-lengthwise transformations, i.e., dissimilar representations of information reveal different results.
- Euclidean distance measures put up unevenly weigh underlying factors.
- The algorithm fails for categorical data and is applicable only the mean is defined.
- Unable to handle noisy data and outliers.
- The algorithmic rule fails for a non-linear data set.
Termination
That brings the States to the finish of unattended learning algorithms, k-agency clustering. We have studied the unsupervised technique that is a case of machine learning in which machines are trained using unlabelled data. Furthermore, we discussed clustering which in simpler words is the process of dividing the datasets into groups, consisting of similar data points. It has various uses, popular ones existence Amazon's recommendation system and Netflix's movie recommendations. Wiggly on we learned about our principal blog topic K-agency clustering algorithmic rule, its algorithmic steps and implied it using a dummy dataset. We also enforced the algorithm using its code in Python and R. Lastly, we unnatural all but the challenges of the algorithm followed by its applications, advantages and disadvantages.
You may select an overview of more machine acquisition algorithms here.
Was this information helpful to you to understand this algorithm? Let us know your feedback!
People are also reading:
- Automobile Learning Certifications
- Motorcar Learning Books
- Machine Learning Interview Questions
- What is Machine Eruditeness?
- How to get over a Machine learning Engineer
- Machine Learning Frameworks
- Decision Tree in Machine Scholarship
- Auto Learning Applications
- Difference between AI and Machine Learning
- Difference of opinion between Machine Acquisition and Wakeless Learning
DOWNLOAD HERE
Understanding K-means Clustering in Machine Learning Free Download
Posted by: larosefriard1941.blogspot.com
Post a Comment for "Understanding K-means Clustering in Machine Learning Free Download"